
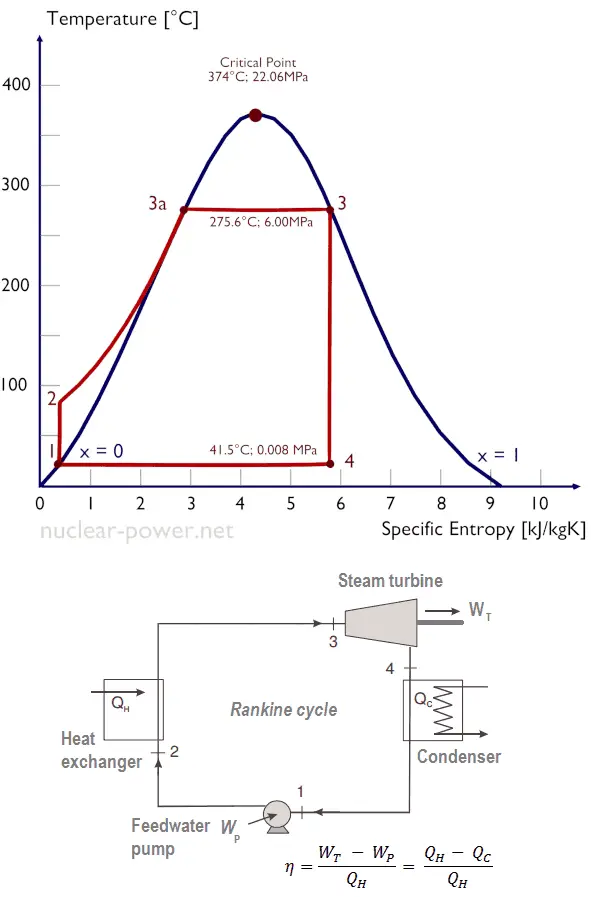
Specific entropy generation is defined as the total entropy generation rate per unit flowrate of the fuel It is found that the thermal efficiency inversely correlates with specific entropy generation, and minimization of specific entropy generation is identical to maximization of thermal efficiency. Minimizing the entropy generation does not lead to an improved thermal efficiency. Numerous studies have indicated that neither the rate of heat input nor the power output in a thermal power plant is treated as a fixed parameter. Maximum reduction in entropy takes place along the line (6-1) when steam condenses in the condenser and loses its kinetic energy at low temperature. Isentropic Compression: Condensed liquid flows to the suction side of the boiler feed pump and the cycle begins again.Įntropy creation: Maximum entropy is added along the line (3-4) when water converts to saturated steam at constant temperature and pressure and breaks its intermolecular bonds and thereafter when superheat is added to steam along line (4-5). Along the isobar (6-1) the heat content of the wet steam is rejected in the condenser. Thus, the expanded superheated steam becomes wet steam again, x=0. As steam expands, its pressure and temperature decrease substantially. Isentropic Expansion: The superheated steam expands through flowing the turbine (5-6) and converts into mechanical energy and runs the turbine. The saturated steam becomes superheated steam beyond point 4, it is heated further to add superheat (4-5). As heat is added to the wet steam its dryness fraction rises to the value of x=1. Isobaric Heat Transfer: As the water begins boiling, pressure and temperature remains constant while its dryness fraction rises along line (3-4).
The temperature rises until attains the saturation temperature belonging the given pressure (2-3). The entropy increase through the pump is neglected (1-2) The liquid water is warmed up until its saturation temperature.

The high-pressure water flows into the steam boiler (2). The boiler feed pump (1) does work on the water increasing its pressure and temperature adiabatically.
#Workdone rankine cycle by ethalpy plus#
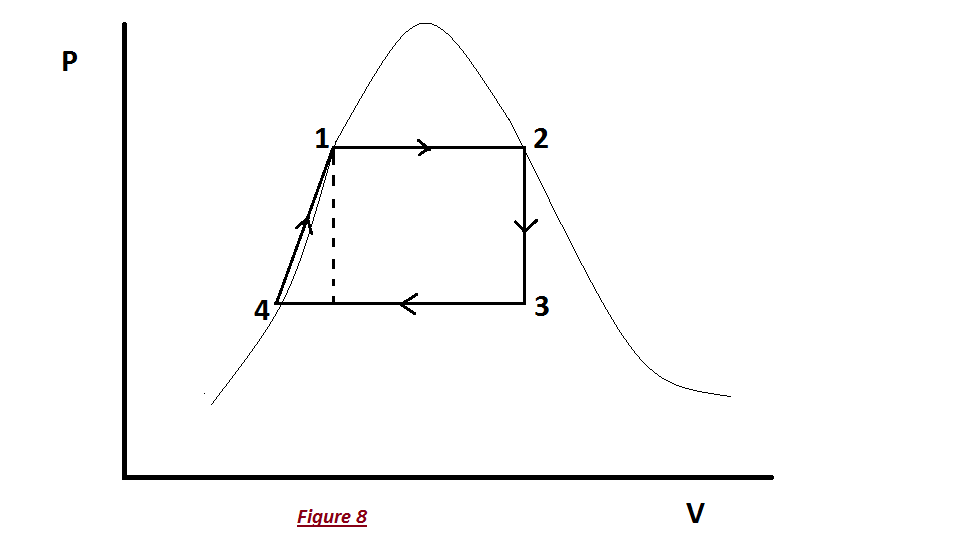
In effect, it says that the energy into the control volume consisting of the entering enthalpy, kinetic energy, and potential energy plus any heat crossing the boundary equals the exiting enthalpy, kinetic energy, and potential energy plus the work output of the control volume.įig 2 simplifies Fig 1 for the case of reversible adiabatic turbines, compressors and pumps.Image 1 – Rankine cycle Image 2 – Mollier diagram Fig 1 is a generic control volume that can be simplified to represent the control volumes for the turbine, pump, condenser, and boiler of the Rankine cycle. So does $W$ in the efficiency really equal $W_$. However, this doesn't seem to exploit the $PV$ work that occurs when the water vapor expands (i.e., during the isobaric portions of the cycle) in any way. Looking at real-life implementations of the Rankine cycle, it looks like all the work is extracted in the turbine, and some additional work is required in the pump: My question is about what the work $W$ in $e = W/Q_h$ actually refers to. Moreover, Schroeder calculates the efficiency by referring to tables of enthalpies (so that he never has to worry where the work happens in the cycle). I know that efficiency $e = W/Q_h = 1 - Q_c/Q_h$, and the total $PV$ work done during the process is represented by the area enclosed by the cycle. I am trying to understand Schroeder's treatment of heat engines, and am having a very hard time understanding the Rankine cycle.


 0 kommentar(er)
0 kommentar(er)
